積分順序の変更を伴う重積分をしましょ～よ！

みなさ～ん！

積分順序の変更を伴う重積分，やってますか？

……

地獄に落ちろ！！！！！！！！！！

皆さんこんにちは，キハダです。

このブログ，めちゃくちゃ放置してました。本当にごめんなさい。

さて，今回はタイトルにある通り，「積分順序の変更を伴う重積分」をやっていきたいな，と思っています。

以下，問題文です。

$D = \{(x,y) | 0 \leq x \leq 1, x \leq y \leq 1\}$ のとき，次の重積分の値を求めよ．積分順序を変更してもよい．

$\displaystyle \int\!\!\!\int_D \sin (\pi y^2) dxdy$

この問題は，某入試問題から引っ張ってきました。問題があれば取り下げます。

さて，こちらですが，正直に書くとこうなりますよね。

$\displaystyle \int_x^1\!\!\!\int_0^1 \sin (\pi y^2) dxdy$

このまま中→外と積分しても， $x$ が残って結局正解が出たこととはなりません。
そこで，「積分順序を変更する」という工程が必要となってくるわけです。

まず，積分順序を交換する際，分かりやすくするために積分範囲についてグラフを図示してみます。すると，以下のようになります。*1

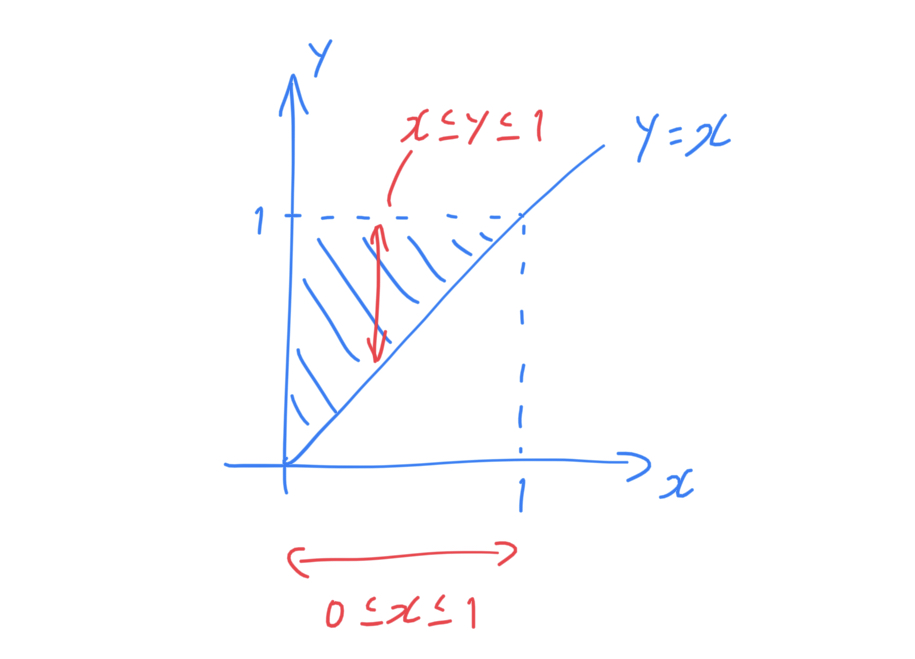
f:id:K1HDA:20210725031513p:plain — 順序変更前

（バリバリ手書きで申し訳ないです。）
ここから，積分順序を変更するために， $x$ から $y$ に基準を変えます。すると，以下のように図示できます。

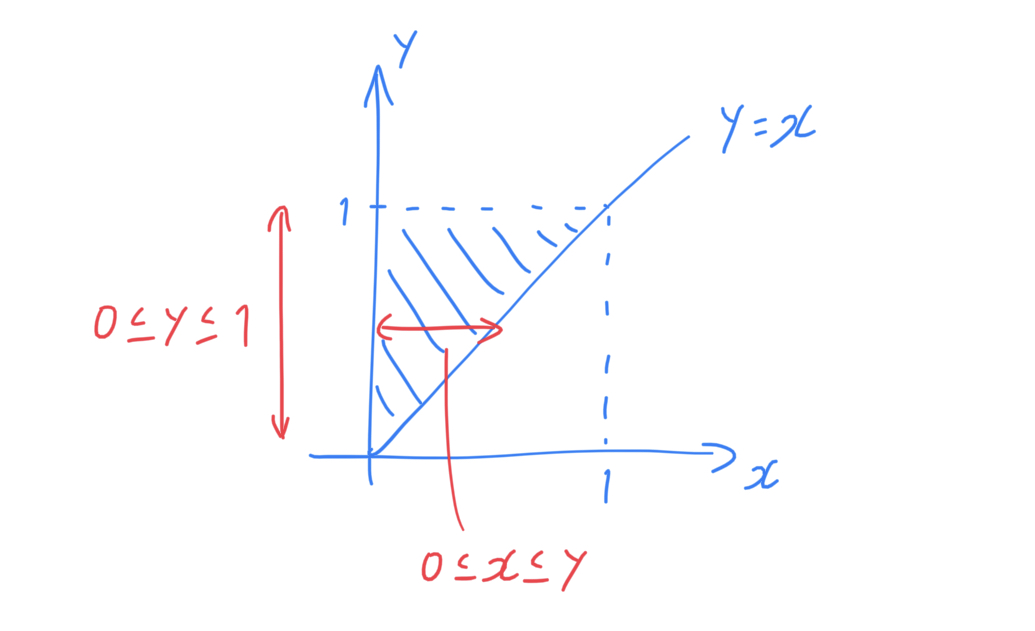
f:id:K1HDA:20210725031838p:plain — 順序変更後

これを式に書き示すと以下のようになります。

$\displaystyle \int_0^1\!\!\!\int_0^y \sin (\pi y^2) dxdy$

あとはこれを積分していきます。

$\displaystyle \begin{eqnarray} && \int_0^1\!\!\!\int_0^y \sin (\pi y^2) dxdy \\ &=& \int_0^1 [ x \sin (\pi y^2) ] _0^y dy \\ &=& \int_0^1 y \sin (\pi y^2) dy \\ \end{eqnarray}$

ここで， $\pi y^2 = u$ とおき，置換積分を適用させます。
すると， $du = 2y \pi dy$ ，積分範囲は $0 \leq u \leq \pi$ となり*2，これらを式に書き替えると，以下のようになります。

$\displaystyle \frac{1}{2\pi} \int_0^\pi \sin u du$

あとはこれを同じく積分するだけです。

$\displaystyle \begin{eqnarray} && \frac{1}{2\pi} \int_0^\pi \sin u du \\ &=& \frac{1}{2\pi} [ - \cos u ]_0^\pi \\ &=& \frac{1}{2\pi} ( - \cos \pi + \cos 0 ) \\ &=& \frac{2}{2\pi} \\ &=& \frac{1}{\pi} \end{eqnarray}$

よって，答えは $\displaystyle \frac{1}{\pi}$ となります。たぶん。間違ってたら教えてください。

順序変更を伴う重積分は，大学数学の範囲ではよく使われるので（主に理学・工学関連では特に），覚えておいて損はないと思います。

今回は以上です。それでは。

*1:グラフの形が $y=x$ となる理由については， $x$ と $y$ の範囲をそれぞれ見てあげればたぶん分かるかと。 $x$ は0から1まで， $y$ は $x$ から1までなので，原点を通り，かつ $(x,y) = (1,1)$ を通る直線は $y=x$ であるということは自明に分かることです。

*2: $y$ の範囲は $0 \leq y \leq 1$ なので，これを $u = \pi y^2$ に代入することで求まります。範囲の最小値は $y$ に0を代入し $\pi \cdot 0^2 = 0$ ，範囲の最大値は $y$ に1を代入し $\pi \cdot 1^2 = \pi$ となります。

キハダの雑記

何気ない日常を記録していきます。

積分順序の変更を伴う重積分をしましょ～よ！